Anwendung der Hubbert´schen Peak-Oil-Theorie auf Gold
12.05.2010 | Dr. Jürgen Müller
I. Einleitung
Dr. Marion King Hubbert (1903-1989) war ein amerikanischer Geologe, der von 1943 bis 1964 für Shell arbeitete und in dieser Zeit seine Peak-Oil-Theorie entwickelte. Diese besagt auf einen Nenner gebracht, dass sich die Produktionskurve von Öl in Form einer Glockenkurve entwickelt. Im Grunde müsste diese Theorie längst "Peak-Wahrheit" genannt werden, da Hubberts Vorhersagen eindrucksvoll durch die Realität bestätigt wurden. Fakt ist, dass sich keine Produktionskurve einer endlichen natürlichen Ressource immer weiter steigern läßt oder unbegrenzt lange auf einem hohen Niveau verharren kann. An einem bestimmten Punkt lassen Geologie und Technik keine weitere Produktionsausweitung mehr zu und es kommt nach einem Peak oder einem Plateau wieder zu einem Abfall der Fördermengen [1].
Unsere Erde ist ein endlicher Raum mit zwingend endlichen Ressourcen. Immer wieder kommt es an diesem Punkt zumeist zwischen Ökonomen und Ingenieuren/Geologen zum Streit. Erstere bemühen immer wieder das Grundprinzip von Angebot und Nachfrage und argumentieren, dass höhere Preise (d.h. größere Nachfrage) auch die Förderung wieder anheben würden. Sicherlich gilt dies für Güter des produzierenden Gewerbes. Leider gibt es im Bereich Ressourcenförderung jedoch viele Beispiele aus der Vergangenheit, die diese ökonomische Argumentation widerlegen, z.B. die Goldförderung des einstigen Hauptförderlandes Südafrika [2]. Obwohl der Goldpreis seit 1971 nicht mehr statisch an den Dollar gebunden war und bekannterweise bis 1980 ein dediziertes Peak bildete, ging die Förderung in Südafrika nach einem Peak im Jahr 1970 in dieser Zeit beständig nach unten, d.h. höhere Preise bewirkten explizit keine höhere Förderung. Auch die aktuelle Vervierfachung des Goldpreises in Dollar, verbunden mit einem Verfall des Randwertes, vermochte es nicht, diesen dramatischen Sinkflug zu stoppen.
In diesem Artikel soll in einem ersten Schritt die Hubbert-Theorie erläutert und nachfolgend auf die Goldförderkurve angewendet werden. Hubbert selbst betonte in seinen Schriften immer wieder, dass seine Mathematik auch auf mineralische Rohstoffe (sprich Metalle) anwendbar ist.
II. Bestimmung der kumulierten Gesamtfördermenge Q∞
Die Hubbert"sche Mathematik ist im Grunde recht simpel und beruht auf der Logistischen Funktion, die der belgische Mathematiker Verhulst 1838 zur theoretischen Beschreibung des Bevölkerungswachstumes entwickelt hatte [3]. Bevölkerungsentwicklung und Ölförderung hängen insofern logisch zusammen, als dass beide Wachstumskurven linear von den freien, noch zur Verfügung stehenden Kapazitäten abhängen. Im ersten Fall von der freien Kapazität der Erde, noch weitere Menschen zu ernähren und im letzteren Fall von dem Teil des Öls, welches noch "frei" zur Förderung in der Erde verblieben ist. Gehen die freien Kapazitäten zur Neige, sinkt auch die Geburten- bzw. Förderrate. Ein bildlicher Vergleich: Bei einer Ketchup-Flasche kommt zu Beginn das Ketchup oftmals wie ein Schwall geschossen, während man die letzten Tropfen mühsam herausschütteln- und klopfen muss. Nicht anders verhält es sich bei der bergbaulichen Gewinnung jedwelcher endlichen natürlichen Ressource.
Erster Kernpunkt der Theorie ist die Bestimmung der kumulierten historischen Fördermenge, d.h. der Menge, die in der Vergangenheit bereits gefördert wurde, plus der Menge die in der Zunkunft vermutlich noch gefördert werden wird. Geologen nennen diese Menge "Q" von (ausgesprochen) "qumulative". Die jährliche Produktionsrate einer Ressource wird mit "P" bezeichnet (für Produktion). Ohne an dieser Stelle auf die Herleitung der zugrunde liegenden Mathematik einzugehen [4]: Trägt man das Verhältnis von P zu Q in Prozent in Abhängigkeit von Q auf, so erhält man eine Kurve, die am Beginn des Produktionszykluses stark variiert, in ihrem weiteren Verlauf jedoch eine Gerade bildet, die man in die Zukunft verlängern kann und damit die zu erwartende Gesamtfördermenge Q∞ (Q unendlich) ermitteln kann. Abbildung 1 zeigt diese sog. "Hubbert-Linearisierung" für die bisherige globale Goldförderkurve.
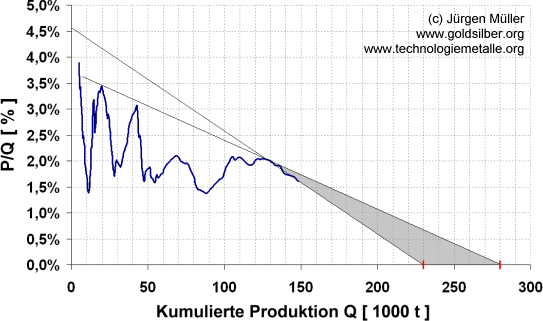
Abbildung 1: Hubbert-Linearisierung für Gold und sinnvolle Extrapolationen in die Zukunft [5]
Da die bisherige Goldförderung stark von geologischen und politischen Ereignissen geprägt war, ergaben sich in der Vergangenheit 4 Unterzyklen, die an anderer Stelle eingehend analysiert wurden [5]. Diese Unterzyklen finden sich auch in Abb. 1 wider. Seit 1968 ergibt sich jedoch eine Gerade, die - in die Zukunft verlängert - eine Gesamtförderung Q∞ von 230.000 Tonnen Gold impliziert. Verbindet man in charttechnischer Manier die Hochpunkte der P/Q-Kurve, so ergibt sich ein optimistischeres Szenario von 280.000 Tonnen. Bisher wurden (je nach Quelle) ca. 157.000 [6] bis 180.000 [7] Tonnen Gold in der Menschheitsgeschichte gefördert. Optimistischerweise kann man also 123.000 Tonnen Gold erwarten, die in der Zukunft noch förderbar sein werden (280.000 minus 157.000 Tonnen).
Der zweite Schritt der Hubbert-Theorie stellt die klassische schulische Integralrechnung auf den Kopf. Musste man hier zu einer bekannten Funktion x=f(y) die Fläche unter der Kurve berechnen, kennen wir durch die Hubbert-Linearisierung die Fläche unter der Kurve (d.h. Q∞) und suchen die dazugehörige Funktion P inAbhängigkeit von der Zeit t. Theoretisch gibt es jedoch zu einer bekannten und endlichen Fläche Q eine unendlich grosse Zahl von möglichen Funktionen. Hubbert argumentierte jedoch, wenn der übergeordnete Produktionszyklus zu ca. 1/3 bekannt ist, d.h. in der Vergangenheit liegt, man den "passenden" Produktionsverlauf mit hinreichend grosser Wahrscheinlichkeit bestimmen kann.
III. Bestimmung der kumulierten Förderkurve mit einer Logistischen Funktion
Um diese zur bisherigen Förderkurve und zu Q∞ passenden Funktion bestimmen zu können, stellt man zunächst die aufaddierten jährlichen Fördermengen gegen die Zeit dar. Die Produktionskurve einer jeden endlichen Ressource nimmt in dieser Grafik einen S-förmigen Verlauf ein. Die Förderung beginnt irgenwann in der Vergangenheit bei null, durchläuft einen Wendepunkt und sättigt sich irgendwann in der Zukunft bei einem Wert Q∞. Mit der mathematischen Methode der kleinsten Quadrate [8] kann man an diese bisherige Förderkurve eine Logistische Funktion anpassen, sodass sich eine möglichst geringe Abweichung zwischen der Realität und dem mathematischen Modell ergibt. Führt man diese Angleichung für die bisherige Goldförderkurve unter Verwendung eines optimistischen Wertes von Q∞ = 280.000 Tonnen aus, so ergibt sich der in Abbildung 2 dargestellte Kurvenverlauf.

Abbildung 2: Bisherige aufaddierte Goldförderkurve, mit Logistischer Funktion für Q∞ = 280.000 Tonnen bestmöglich approximiert.
Im unteren Bereich von Abbildung 2 wird die qualitative Abweichung zwischen Modell und Realität dargestellt. Es ist interessant zu sehen, dass die Kurve bis 1971 eine bemerkenswerte Übereinstimmung mit der mathematischen Funktion ergibt. Die größten Differenzen ergeben sich erst seit der Zeit, in der die Gold-Papiergeld Fixierung aufgehoben wurde. Die Interpretation hieraus ist, dass das Preispeak von 1980 eine Förderung induzierte, die über das zu erwartende Maß weit hinausging und die reichsten Erzlagerstätten schneller zur Erschöpfung brachte bzw. bringen wird, als dies unter normalen wirtschaftlichen Bedingungen wohl der Fall gewesen wäre. Noch anders ausgedrückt rückte dieser Preispeak das Förderpeak auf der Zeitskala um einige Jahre nach vorne, genauso wie es in Südafrika der Fall war, als staatlich-steuerliche Stimulierungen in der Apartheid-Ära die Förderung ankurbelten.
IV. Hubbert-Kurve für Gold
Differenziert man die integrierte Form der Logistischen Funktion aus Abbildung 2 nach der Zeit, erhält man die bekannte Glockenkurve in Abhängigkeit von der Zeit, die in Abbildung 3 dargestellt ist.

Abbildung 3: Zeitlicher Verlauf der theoretischen Glockenkurve für die globale Goldförderung.
Wie zuvor erwähnt führte der letzte Unterzyklus seit 1980 die Förderung weit über das theoretische Modell hinaus. Die modellierte Kurve weist ein Förderpeak im Juli 2007 bei einem Wert von 1.841 Tonnen auf. In der Realität fiel das Förderhoch auf das Jahr 2003 bei 2.590 Tonnen [9]. Dies ist ein Phänomen, welches auch für andere Ressourcen in der Vergangenheit zu beobachten war. Das Peak fiel oft einige Jahre zu früh und einige Produktionseinheiten zu hoch aus. Selbst unter optimistischen Prämissen ergibt also das Hubbert-Modell ein theoretisches Peakjahr, welches bereits in der Vergangenheit liegt, nämlich im Jahr 2008. Das reelle Peak von 2003 erfolgte 5 Jahre früher, genauso wie z.B. das Peak der U.S. Crude Oil Förderung 1970 bei 3,52 Milliarden Barrels [10] erfolgte, das Logistische Wachstumsmodell jedoch für das Jahr 1976 einen Peak-Wert von nur ca. 3 Milliarden Barrels vorhersagte [11].
V. Optimistisches Szenario
Es soll nochmals explizit betont werden, dass das in Abbildung 3 veranschaulichte Modell ein aus heutiger Sicht optimistisches Szenario darstellt. Die amerikanische geologische Statistikbehörde U.S. Geological Survey (im Folgenden "USGS") gab die aktuellen geologischen Goldreserven in ihrem Goldreport von 2009 mit 47.000 Tonnen an [12], wobei der Begriff "Reserven" diejenigen bekannten Vorkommen bezeichnen, die mit dem aktuellen Stand der Technik und dem aktuellen Preisniveau von Gold wirtschaftlich gefördert werden können. Weiterhin wurden 53.000 Tonnen Ressourcen ausgewiesen [12], d.h. Vorkommen, bei denen aktuell die Wirtschaftlichkeit nicht gegeben ist. Addieren wir diese Zahlen: Bisherige Förderung 157.000 Tonnen + bekannte Reserven 47.000 Tonnen + bekannte Ressourcen 53.000 Tonnen = 257.000 Tonnen. D.h. das hier präsentierte Modell läßt Spielraum für weitere 23.000 Tonnen, die in der Zukunft noch gefunden werden müssen. Weiterhin unterstellt das Modell, dass alle bekannten Reserven auch tatsächlich abgebaut werden können und sämtliche bekannten Ressourcen sich zu Reserven entwickeln werden, die ebenfalls wiederum zu 100% abgebaut werden können. All diese optimistischen Annahmen sind also notwendige Voraussetzung für das hier beschriebene 280.000 Tonnen Modell.
Weiterhin vernachlässigt das Modell die kommenden Effekte von Peak-Oil, die den Bergbau insgesamt verteuern und begrenzen werden. Der frühere USGS Präsident V.E. McKelvey schrieb in diesem Zusammenhang bereits im Jahr 1972, dass "der Ver- und Gebrauch von Mineralien (d.h. Metallen) und Brennstoffen (d.h. Öl, Gas, Kohle und Uran) jeweils essentiell für die Verfügbarkeit und den Gebrauch des anderen ist" (freie Übersetzung des Autors) [13]. Mit anderen Worten: Ohne Öl keine Metalle und ohne Metalle kein Öl (bzw. weniger Öl, weniger Metalle).
VI. Auswirkungen auf die zukünftige Kaufkraft von Gold
Unter Geologen ist unbestritten, dass die Logistische Gleichung von Verhulst aus dem Jahr 1838 ein sehr gutes mathematisches Werkzeug darstellt, um die zukünftigen Verläufe von Produktionskurven natürlicher endlicher Ressourcen zu approximieren.
Das hier diskutierte Modell impliziert, dass das Produktions-Peak von 2003 mit 2.590 Tonnen der historische Wendepunkt der Goldförderung war und in der Zukunft mit einer tendenziell fallenden Produktion gerechnet werden kann. Dass diese Hypothese in der Tat auch durch aktuelle geologische Entwicklungen untermauert wird, wurde an anderer Stelle durch den Autor diskutiert [5,14,15].
Es ist demnach damit zu rechnen, dass eine steigende Nachfrage auf ein kontinuierlich sinkendes Angebot treffen wird. Gold sollte daher auch nach der aktuellen systematischen Krise des expontiellen Zinspapiergeldes ein lohnendes Investment bleiben. Gleiches gilt inhaltlich auch und noch mehr für Technologiemetalle, die im Gegensatz zu Gold wirklich ge- und verbraucht werden. Ohne Metalle kein Öl, ohne Öl keine Metalle.
© Jürgen Müller
www.goldsilber.org, www.technologiemetalle.org,www.werteinlagerung.de
In eigener Sache: Dieser Artikel erschien bereits (aus Platzgründen) in stark gekürzter Form im Smart Investor Magazin, Ausgabe 5/2010. Die Redaktion des Smart Investor verweist auf die Möglichkeit des kostenlosen Probeabonnements. In den kommenden Woche publiziert der Autor Hubbert-Kurven von weiteren Metallen auf goldseiten.de.
[i]Referenzen:
[1] J. Müller: "Glockenkurven", www.goldseiten.de/content/diverses/artikel.php?storyid=7409
[2] Minenkammer Südafrika, www.bullion.org.za/Econ&Stats/HistoricalGoldData2.htm
[3] P.-F. Verhulst: "Notice sur la loi que la population poursuit dans son accroissement", Correspondance Mathematique et Physique, Vol. 10, S. 113-121, 1838
[4] M.K. Hubbert: "Techniques of Prediction as Applied to Production of Oil and Gas", U.S. Department of Commerce. NBS Special Publication 631:16-141, 1982, www.goldsilber.org/artikel/hubbert-1982.pdf
[5] J. Müller, H.E. Frimmel: "Numerical Analysis of Historic Gold Production Cycles and Implications for Future Sub-Cycles", Open Geology Journal, Vol. 4, S. 29-34, 2010, www.goldsilber.org/artikel/29TOGEOJ.pdf
[6] M.W. George, "2007 Minerals Yearbook Gold [advance release]", S. 31.2, September 2009, http://minerals.usgs.gov/minerals/pubs/commodity/gold/myb1-2007-gold.pdf
[7] H.E. Frimmel, "Earth"s continental crustal gold endowment", Earth and Planetary Science Letters, Vol. 267, S. 45-55, 2008
[8] Wikipdia, http://de.wikipedia.org/wiki/Methode_der_kleinsten_Quadrate
[9] USGS, http://minerals.usgs.gov/minerals/pubs/commodity/gold/gold_mcs05.pdf
[10] http://tonto.eia.doe.gov/dnav/pet/hist/mcrfpus1a.htm
[11] K.S. Deffeyes: "Beyond Oil", Simon & Schuster, New York, S. 41
[12] USGS, http://minerals.usgs.gov/minerals/pubs/commodity/gold/mcs-2009-gold.pdf
[13] V.E. McKelvey: "Mineral resource estimates and public policy", American Scientist, Vol. 60, no. 1, S. 32-40, 1972.
[14] J. Müller: "Peak Gold", Smart Investor 10/2008, S. 22-26, www.goldsilber.org/smartinvestor_10-2008.pdf
[15] J. Müller: "Zyklik der globalen Goldförderung", Messemagazin 2009/2010, Edelmetall & Rohstoffmesse München 6.-7.11.2009, S.138-139, www.goldsilber.org/artikel/20091106.pdf


